Generating tickets for tambola — or bingo, or housie, or whatever

Recently, I’ve been fiddling with clojure and having some fun. It has some pretty powerful abstractions that allow neatly expressing ideas. I came across tambola tickets in some internal discussions, and thought it’s an interesting problem to solve. And, what better way to flex one’s clojure muscles than to use it to have some fun?

By the end of this post, you’d know a little bit about transforming ideas into code, and also about how easy clojure makes it look. And if you’re lucky enough to be a novice, you may even pick up a few new clojure functions along the way.

Exploring the problem

The curious case of tambola tickets

Ignoring tambola as a game, let’s just focus on the tickets. The tickets have some interesting characteristics:

1. A ticket is made up of a grid of 3 rows and 9 columns
2. In each ticket, 15 of the cells have unique numbers ranging from 1–90
3. No row has more than 5 numbers
4. No column is empty
5. The numbers in every column are in ascending order from top to bottom
6. The first column has numbers 1–9, the second column onwards have numbers 10–19, 20–29, and so on, and the last column only has numbers 80–90.

This seems to be a deceptively challenging problem. I found a few resources — 2 github repos, a website, and a forum post from 2013 on approaches. The 2 repositories have 200 and 400 lines of code each, and still have their issues. One of the approaches needs backtracking and is really hard to follow, while the other produces invalid tickets like these:

At first glance, the problem seemed very sophisticated. I was overwhelmed with the various combinations of the grid patterns. Any strategy needs selection of certain boxes to fill under some constraints.

Thinking about solutions

A very necessary and underrepresented step in making software

Before we jump into coding, let’s think about the problem. Let’s try to reduce it into composable building blocks to weed out the complexity. There’s 2 problems: figuring out the 15 boxes to fill in, and then filling those in with numbers.

While thinking about this, I called my sister up — all excited about the challenges. I do rubber duckying (a lot), where I explain my thoughts to another person; it helps me think clearly. I explained the requirements of picking the 15 boxes, and asked her for ideas.

She told me what she’d do to pick one set of 15 boxes: pick alternate boxes throughout the grid, and fill 1 more random box when there are only 4 boxes in a row. For example:

It was pretty cool to see a human way of creating one valid grid pattern. Later on, I’d tweak this to my needs, but this was the seed — the first idea, and a hint of a solution!

NOTE: If you’re interested in solving puzzles like I am, be sure to follow her on Instagram. She comes up with new puzzle games every month — each with their own set of rules — and then proceeds to create new puzzles for it every day of that month! No wonder I wanted to talk to her, right? Go check her out!

While talking with her, I also figured out that once we have a particular set of 15 boxes figured out, we can essentially create other valid sets of 15 boxes by swapping a row or a column of the grid with another. A small step for us; a giant leap for tambola tickets!

Generating a valid grid

And keeping it simple and brief

Fair warning, there’s going to be a little bit of clojure code ahead. But the ideas themselves are very simple to follow, I promise. Depending on your familiarity with clojure the solution may be enjoyable or overwhelming — try and have fun regardless.

As I pointed out earlier, the first challenge is to generate a valid grid. There’s very little to do when picking a data structure for this — we use a 2d vector which is most similar to a (2d) matrix (or a 2d array, if you will). I wanted a grid to be a 3x9 vector of booleans, which specify whether that position is to be filled in or not. Typing out true and false was annoying so I made it into 1 and0 instead — it was easier to read, too.

Our grid is represented by a 3x9 vector of 1or 0 where 1 is a spot we select to be filled in. To start with, let’s make sure there’s at least 1 spot in every column, and 5 spots in every row to be filled in.

To ensure every column has a spot, we only need the first 2 rows. If we had 2 rows, in the first row, we can fill out the first 5 boxes. To guarantee that every column has a number, while ensuring a single row doesn’t have more than 5 numbers, we can take a second row, and add numbers where there are no numbers in row 1. With these 2 rows, we’ve ensured no column in this grid will be empty.

row-1 [1 1 1 1 1 0 0 0 0]
row-2 [_ _ _ _ _ 1 1 1 1]

Now, when no row has more than 5 numbers, and only 15 numbers can exist in the 3 rows, every row has to have 5 numbers exactly. Since we filled in 5 numbers in row 1, we’re good. Let’s look at row 2. The 1 can go into any of the empty spaces we’ve left out. Essentially, we want the 1 to be shuffled into any of the 5 spaces at the start of row 2, and the rest can remain 1s. Now, how about the 3rd row? It can be any row with five 1s and four 0s. We can essentially shuffle any of the 2 rows and get the 3rd row — it doesn’t matter.

Writing in clojure feels very natural — it’s almost like our ideas turn into code, without much to process in between. There’s very little ceremony to express oneself. Let’s look at how this maps to clojure code:

Isn’t it really simple to follow? shuffle does exactly what you think, and into inserts elements from the second vector into the first vector. We use into to create the 2nd row by combining the first part with a 1 at a random position in the first five boxes, and adding the four 1 s at the end. And that’s it, putting the 3 rows into a vector gets us our 2d vector, the grid!

Writing in clojure feels very natural — it’s almost like our ideas turn into code, without much to process in between. There’s very little ceremony to express oneself.

Now, this generates a few valid grids, but the first five boxes in the first row, and the last four boxes in the second row are always 1 s. To change this, we can shuffle the rows around. Remember we could shuffle numbers in a vector with shuffle? Since our grid is a vector of vectors, we can shuffle that too!

But even if we did that, one of the rows will always have the first five boxes have numbers. To create all possible configurations, we need to also shuffle columns. But shuffle only shuffles in 1 dimension — how do we shuffle 2 dimensions? If only we could shuffle columns as easily as we could shuffle rows. But wait! We’re just dealing with a matrix — and we can transpose a matrix, changing its rows into columns and vice versa!

Let’s write a transpose function and see if we can do a 2d shuffle:

Creating transpose is as simple as composing a few functions in clojure: partial, apply, mapv and vector. partial is a function that takes a function and a subset of its arguments to partially apply them to the function. apply is a function that takes a function and a collection of values and supplies the values in the collection as individual arguments to that function. mapv is a map but returns a vector instead of a sequence. vector just returns a new vector containing its arguments.

Being able to create such functionality by just composing a few powerful functions is one of the amazing things about clojure. Imagine writing transpose in another language of your choice!

When we do a 2d shuffle, we essentially transpose the grid, shuffle it once, and transpose it again, and shuffle it once again. The first shuffle shuffles the columns, and the second shuffles the rows, so we do a 2d shuffle. comp is a function that allows for composing functions together right-to-left. We use comp to say shuffle-2d is actually just a composition of a shuffle and transpose twice, back to back — pretty simple!

There’s no conditions, or backpropagations, and we didn’t need to write pesky long algorithms to come up with a solution. We thought of a simple idea, and expressed it in code, and voila! We have a solution that works! And it’s 7 lines of code!!!

Here’s a few grids generated using the function, for reference:

1 0 1 1 0 0 1 0 1
0 1 1 0 1 1 0 1 0
1 1 1 1 1 0 0 0 0

1 1 1 1 0 1 0 0 0
0 1 1 1 0 1 0 0 1
0 0 0 1 1 0 1 1 1

0 1 1 0 0 1 1 1 0
1 0 1 1 1 0 0 0 1
0 1 0 0 1 1 0 1 1

1 0 0 1 1 1 0 1 0
0 1 1 0 0 0 1 1 1
0 1 1 0 1 0 1 0 1

0 1 1 0 1 0 0 1 1
0 1 0 0 1 0 1 1 1
1 0 0 1 0 1 1 1 0

0 1 1 0 0 1 1 1 0
1 0 0 1 1 0 1 0 1
0 0 1 0 0 1 1 1 1

Filling in the numbers

A supposedly simpler problem, but interesting in its own right!

Earlier I mentioned that generating valid tickets is a 2-part problem, and it’s absolutely true. To the extent that we could’ve independently worked on this problem without solving the other. Let’s tackle filling a valid grid with numbers.

It’s useful to have a range of numbers to choose from for each column. Given the rules, it’s pretty easy to write this in clojure:

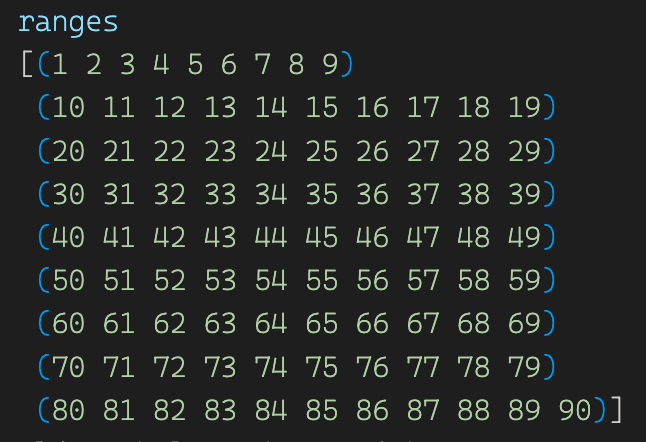
range is a function that takes a start and end (exclusive) to generate a sequence of numbers. ->> is the thread-last macro that helps chain function calls.

To fill the grid, we can just fill every single column. Since we hold the grid as a vector of rows, transpose as we defined earlier, is really helpful. We can transpose the grid, fill every column, and transpose it back to get the filled grid — neat! If we had a function filled that could return a filled column given a grid column with 1 s and 0 s, we could write out fill function like this:

Let’s think about what we just described — to fill a grid: we take the grid, transpose it, map every column to a filled column, and transpose it back again. How easy was that to map ideas to code?

But how to get to a filled column from a grid column? We somehow need to know what to fill in, and then fill it in. Let’s tackle them separately, looking only at a single column, given we can simply map our columns.

What to fill depends upon the column index. We need a random set of numbers to fill in, but in sorted order. The number of elements we need to fill also matters. Let’s try to get the fills for a column. We can get the range of numbers we can use, from the ranges value we defined earlier. But we need the index of the column for that. Then we need the count of values we need to fill. This is easy, because we used 0 s and 1 s, because we can just sum the values to get the count of fills in a column. If we did it another way, we can just map them to 1 s and 0 s and get it done anyway.

Let’s see what we’ve written. Take an index, get the numbers that can be filled at that index by using ranges that we defined earlier. This is possible because vectors in clojure are a function of indices to values — pretty cool, isn’t it? Then we shuffle, and take only a few depending on how many 1 s we have in the column. Finally, after taking as many of the shuffled numbers required, we sort them. How easy was that?!

That’s about it. Now comes the actual filling in part. We have a sequence of fills, and a column to fill. How do we do that?

As we fill in numbers, we need to remove them from the fill, while adding them to the column. When we have a 0 in the column, we only add the 0 to the column. We use a function conj in clojure to add a new value to our column. We’re updating 2 values — the numbers that we use to fill, and the column we’re building one cell at a time. So, we need to take both as parameters, and return new versions of both. This looks like a reducer function where the accumulated value is the fills and the filled column.

If the column value is 0, then we just return the numbers, but add the value to the column. Otherwise, we return the rest of the numbers (without the first number), and add the first number from the list of numbers to the column.

Now that we have a reducer function, we can actually reduce the column into a filled column. Since we accumulate both the remaining (empty) numbers and the filled column, we pick just the column after the reduce. The fill function still needs the column index, which we need to get the list of numbers to fill in. We have a handy function called map-indexed which is a map, but takes a function which operates on an index and an item. second is a function that takes the second element in a sequence, which we use to get the new filled column from the reduced output.

Putting everything together, we have:

A few variable names are changed, and the functions are simplified to a few lines each, but the idea is still the same. xs refers to a list of x s, in this case a vector of numbers — or a column. ' represents a changed or a new value, for example: we return a new column xs from filled. fill is now just a simple composition of transpose, map-indexed, and filled. With those out of the way, let’s look at the definitions.

How easy was that to map ideas to code?

We have a function transpose defined which can be shared with the grid. We have a vector ranges which contains fillable numbers by column index. We have a function fill-non-zeroes which reduces over fills and creates a filled column from a fill and a grid. We then have a filled function which takes an index and a column to return a filled column. The fill function takes a grid, and transposes it, maps from grid columns to filled columns, transposes it back, and returns the resulting filled grid.

Putting things together

Do we have valid tickets yet?

As mentioned earlier, creating a ticket is as simple as creating a valid grid and then filling it, so let’s define a function that creates valid tickets:

The complete solution with all parts together looks like this:

Notice that, because we shuffle columns, we no longer need to shuffle the second row. This is because regardless of the position of the 1 in row 2 in any of the first 5 spaces, the column values remain the same — a column with 2 1s, 4 columns with 1 in the first row, and 4 columns with 1 in the last row. Since this doesn’t change, we can further simplify the grid function to be:

Initially, we thought it’s a 2 part problem — generating a valid grid, and filling it. But now, it seems like the generation of a valid grid itself can be broken down into smaller problems. First, we need a permutation of the 1st row, then we can add it as the 3rd row to rows 1 and 2, and then we can do a 2d shuffle to get the final valid grid. Filling the grid comes after. Let’s rewrite grid to be a simple idea to code conversion:

Now that we have a clearer picture of the grid generation, we can simplify ticket generation — first we need a valid grid, then we can shuffle it in 2d, and then fill it. This is as simple as rewriting our ticket function to compose 3 functions instead of 2 as earlier. Looking at everything together, we have:

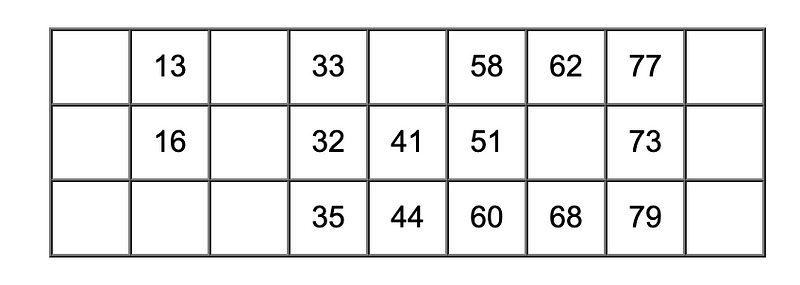
And it totally works! And, we wrote hardly 25 lines of code. Let’s look at some generated tickets (pretty printed):

They follow all the rules (if I do say so myself), and our ticket function can produce any valid ticket! That’s because all the possibilities are embedded. It’s easy to guarantee the characteristics since we designed the solution keeping them in mind. And we built up the solution using well-defined functions whose behavior is guaranteed and deterministic, so not much can go wrong.

To ensure the tickets we generate have the characteristics we designed for, we can add some property-based tests using test.check:

Time to see some test results. I’m so confident in the solution that I’m just going to hope they pass on the first run. How many of these do you think we’ll pass?

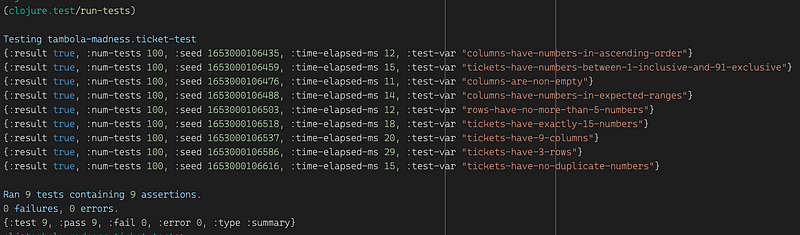
Well, all of them, looks like! Pretty cool — all in a day’s work, too.

Conclusion

All good things must come to an end

It was a lot of fun coming up with a solution — which is very human, and uses some interesting properties of 2d vectors, permutations, and the like. It’s also really amazing that we’re able to express these ideas clearly and concisely in clojure. And how easy was it to create our own transpose and shuffle-2d functions!

I hope you have as much fun with clojure as I did with this little problem. And that translating ideas into code feels as amazing as it does to me.

PS: If you’re interested in a little more fun, try these challanges:
1. rewrite the fill-non-zeroes function without an if
2. generate tickets deterministically (way to get identical tickets on demand)