Implementing a custom collection type in clojure — the leftist heap, a persistent priority queue

As I mentioned earlier, recently I’ve been having a lot of fun with clojure. Usually, its well thought-out and powerful abstractions make solutions to certain problems really simple. For dealing with collections of data, we rarely need beyond what clojure already offers: list, vector, map, and set. For the occasional use, there’s also extensions like queues and sorted sets or maps. And these are very carefully crafted and are bolstered by a plethora of useful functions.

However, there’s the odd time where you need something more. Where the collection types are just lacking in a specific abstraction, and using them feels like fighting the system a lot. In such cases, we’re totally allowed to roll our own types!

By the end of this post, you’d know a little bit about a few things. For one, you’d become familiar with the concept of a class of problems where custom collection types are indeed the right abstractions. If you’re lucky, you’d also see how the right abstractions help simplify solutions. Surely, you’d learn how to implement custom collection types in clojure. If you think that’s cool, you’d also learn how to customize how they’re displayed in the REPL.

In addition, you’d understand the power of the existing collection functions available to you, and how their idiomatic usages help introduce new collection types without much friction. If you’re lucky enough to be a novice, you might even pick up some idiomatic clojure functions to deal with collections along the way.

The case for custom collection types

Can’t we just use the existing collection types?

I recently encountered a problem regarding trades in a stock order processing system. The trades need to match orders by specific rules. In this case, every buy order needs to be matched with the cheapest (and earliest) sell order for the same stock. If we had a collection of sell orders for a stock, there’s a few things we want to be able to do:

1. Add a new sell order
2. Get the best (cheapest and earliest) sell order
3. Remove the best sell order

In essence, these are the only operations we need. For example, there’s no need to iterate over all the orders, remove an order at a specific location, or search for a specific order. There’s a few ways to solve this problem. Let’s look at what we could do with what clojure already provides.

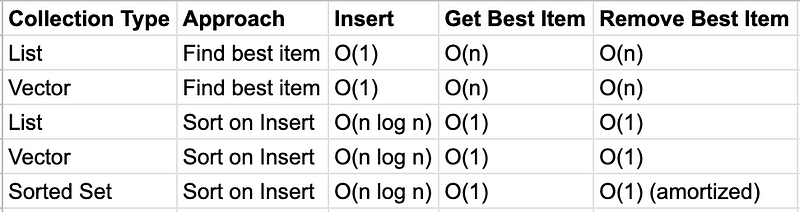
For one, we could just use a list. When getting the best order, we’d search through the list. The problem with this is that when we want to remove the item from the list, we either need to search again, or we’re changing the list too much to remove an item at a specific location in the list. Vectors have a similar problem. Sets do not provide any specific benefits over lists or vectors.

Secondly, we could use a list or a vector, but keep sorting it (using sort-by) after every insert. That way, we don’t need to search for items once while getting, and once while deleting. And if we sort the right way, removing the best item can be a very optimized constant-time O(1) operation. For example, it’s very easy and efficient to remove the first element of a list or the last element of a vector. However, the sorting is a bit expensive. Lists and vectors are both not very efficient at reordering, and end up wasting a lot of structural sharing.

It’s good to know that some collections are optimized for fetching and removing items at one end. For lists, we can use first and rest, while for vectors and queues we have peek and pop. This seems really useful — can we do better? What about sorted collections?

We can use a sorted set (by calling sorted-set-by with a comparator function), and it almost seems to work, except that we both compare and remove items by keys, and we can’t have duplicates. In this problem, we want to compare the sell orders by price and timestamp, but there could totally be 2 orders with the same timestamp. They’re equal by comparison, but a sell order shouldn’t replace any other even if the price and timestamp are equal.

It’s good to know that some collections are optimized for fetching and removing items at one end. For lists, we can use first and rest, while for vectors and queues we have peek and pop.

We could introduce another key into the comparator, but we’re bordering on fighting the system at this point. This is because sorted sets are ordered by key, not value, and here we’re almost confusing the key (used to identify) and value. Another problem is that sets don’t have a way to remove the first or last element like lists or vectors. To remove an element from the set we’d use the disj(oin) function. Using rest would return a sequence, losing all the advantages of the sorted-set.

Is there a better custom collection type?

What if we’re only interested in the best value in the collection? TLDR: Yes!

As it turns out, there’s other collection types which come in handy. For example, the heap is a data structure which has the following performance characteristics:

The heap is tailor-made for this use case where we’re interested in a notion of the best values in a collection. Here, we’re interested in the best sell order in a collection of them. So what better way to model it than a heap? A leftist heap is an unbalanced tree which works by ensuring merges are cheap. Insertion is a merge of a tree with another tree with a single node. Remove is a merge of the left and right trees of the node.

A leftist heap is a priority queue that’s also a functional, immutable, persistent data structure that can maximize structural sharing. Which is why we’re implementing the heap using a leftist tree. I’d encourage you to do your own research on leftist trees to understand them better, as explaining that is outside the scope of this post. However, the implementation itself is simple to follow, and you can evaluate the code in your repl to see how it’s built.

Let’s see what the API for this leftist can look like. On closer inspection, the heap is also functionally a stack. So we can take a peek on and pop it. That takes care of the get-best and remove-best operations, but what about adding a new stock order? In clojure, it’s idiomatic to use conj(oin) to add a value to a collection in the most efficient way, so we can use the same. Using idiomatic functions helps consumers use the functions they know very well with impunity. And, in our case, the existing abstractions map very well — so why introduce new ones? Just reuse — these are powerful abstractions for a reason!

NOTE: When creating leftist, we’re just creating another powerful abstraction (that can be used beyond the scope of this single problem).

Implementing a leftist heap

And making it a custom collection type

We can model the node as a map with a few well-established keys — this is idiomatic as well. The three keys we need are left, right, and value. We can use keywords as keys, which is also idiomatic — we’ll see why in just a second. Since leftist is powered by a merge, we need to write out the merge function. We need a worse? function that compares 2 values and returns true if the first value is worse than the second. Here’s our merge:

We need a helper to determine the rank of a node— this is just the distance to the right node, sometimes called the s-value. We use the :right keyword as a function, because it is! In clojure, keywords are functions that look themselves up in maps. Here node is a map, as we explained above. A cool feature is that if the key is not available, it returns nil, which is what we want in this case. We don’t need to check if the node itself is nil!

A leftist heap is a priority queue that’s also a functional, immutable, persistent data structure that can maximize structural sharing.

Then we have a way to create a node from a value, left and right nodes. The important thing is that in a leftist tree, the rank of the left node is always higher than the right. If not, we swap the left and right nodes. Then all we need to do is use zipmap to merge 2 vectors of keys and values into a map.

Finally, we merge 2 nodes a and b with a functionworse? which compares the values in them. If one of the nodes is nil, we just return the other. We use nil to represent an empty node, which is also idiomatic. If the value of a is worse than that of b, we swap them. We merge the b to the right of a , while keeping the left of a, in order to create a node. Recall that node takes care of swapping the left and right nodes if the rank is not the way it’s supposed to be.

Defining the custom collection type

Implementing some interfaces, and getting a lot for free in return!

So, now we just need to write our leftist as a custom collection type. We can use the deftype macro to do this. We need to implement a few interfaces to get this working. Thankfully, there’s a very nice gist we can use that will help understand the interfaces we need to implement in order to finish our type. I mentioned our heap is persistent and a stack, so we will want to implement clojure.lang.IPersistentStack.

Let’s take a look at how we can implement it. This is pretty straightforward, we only need to use merge when we insert and when we remove the best item. We can just lookup the node with :value when we need to peek into the best item. Notice that we implement the minimum set of methods here, and collection methods like conj and into are automatically made available for us.

Making the custom collection type production-ready

Sprinkling some useful niceties

Creating a leftist is very cumbersome right now, while creating vectors is so simple! Let’s make a more idiomatic constructor to use, that takes a comparator and values and constructs a leftist with those values. This should be simple enough.

Another thing we can do is have a way to pretty print the collection, to notify that it’s a priority queue. This results in some cool REPL outputs.

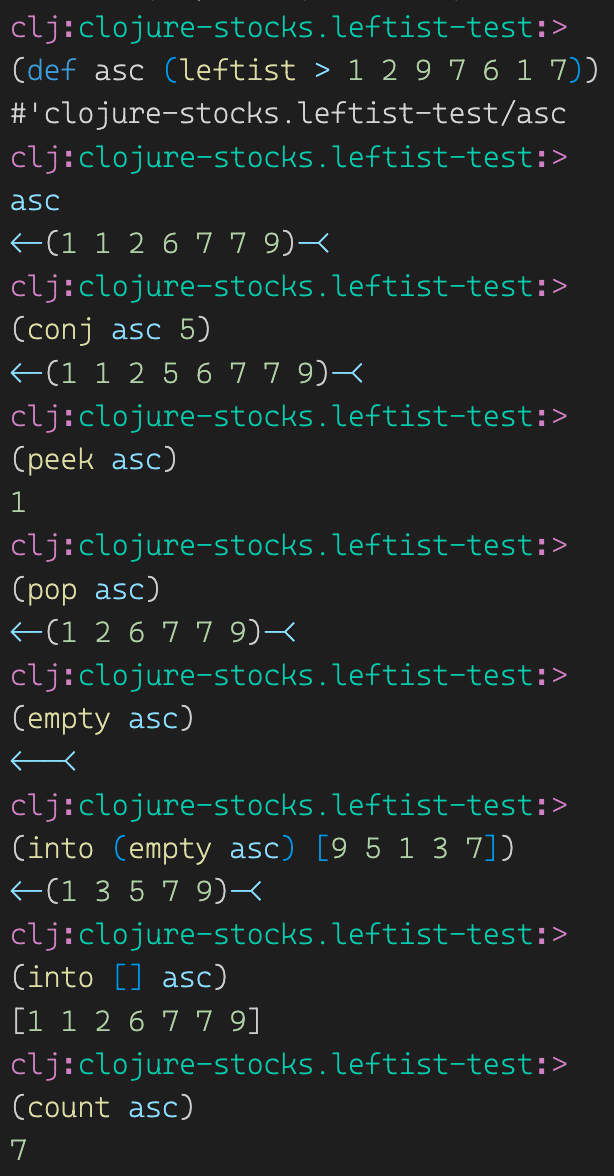
Let’s look at some outputs to see how our new collection works. We can create a leftist with some worse? function and a few values. We can see that internally we use into which uses conj which uses our cons implementation. Additionally, we use peek and pop to see what those return. Notice that they’re all doing the idiomatic stuff — they all return new collections, and never mutate the original collection. Here we go:

Put together, this is how all the code we’ve written so far for our custom collection type looks:

Adding a few tests

When are we ever gonna get away without testing stuff?

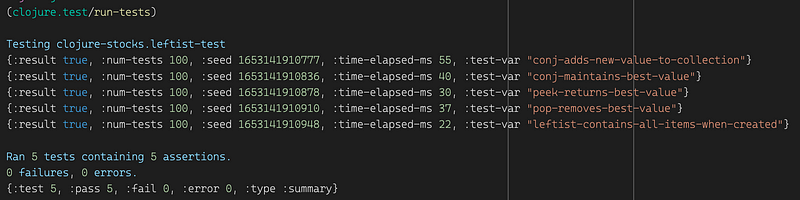
We’re primarily only interested in the above-described 4 functions which is a pretty idiomatic API, so let’s see what we can test about them. Adding a few properties to our implementations never hurt anyone, so let’s get some help from test.check:

A quick run will tell us how well we did. Before you look at it, let me say, I fully expect to pass. Not only did we do wonderfully well in our implementation, but we also did not describe too many properties. Sorry for the spoilers:

Conclusion

Coming up with subtitles is no easy task, it looks like

I hope that gives you an insight into when it makes sense to use custom collections, and how to go about implementing them. Also, how cool is that arrow-based output ?! I stole that from clojure’s own queues — some things are just too awesome to not “use as inspiration” (wink).

It’s inspiring that you stuck with the post until this section, kudos to you! I hope you picked up something useful, and the post delivered on all or at least most of its promises. I’m always amazed by the power and simplicity of clojure’s abstractions. Even when we want something custom, we’re still supported by the same idioms. Do you think that’s accidental?

BONUS FUN: Is there an abstraction you can think of that can be reused between our node and merge functions? What’s something we do in both?