Understanding isomorphisms by writing some in TypeScript
I have mentioned isomorphisms before, but left it at a high level. Is there only one isomorphism from a type to another? How do we write them? Time to dig in.

In my last post I touched upon isomorphisms. They're part of category theory but as I mentioned before, in programming, types are representative sets (or categories). Today we'll understand isomorphisms more by writing some in TypeScript.
NOTE: All of the code used here is available as a public GitHub repo that you can clone and play with on your local machine. Feel free to open up a TS Playground and keep playing with live code there to follow along.
Type definitions
As I always mention, ideas in code are shared via abstractions. Let's come up wth an abstraction for an isomorphism. We can start with a simple type that represents a morphism, which is just a function that transforms from a source type to a target type:
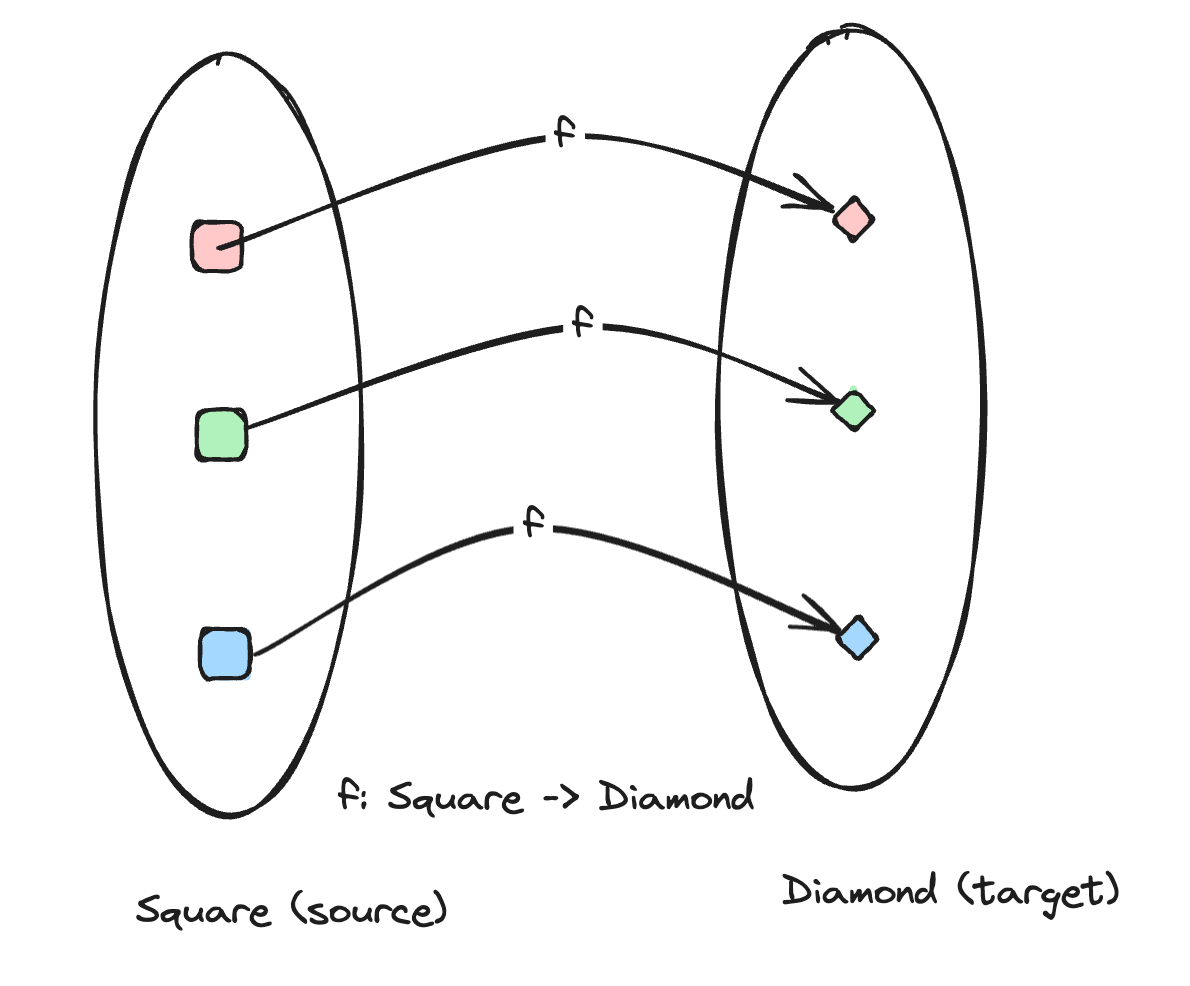
export type Morphism<S = any, T = any> = (a: S) => T;
export type Source<M extends Morphism> = M extends Morphism<
infer S,
any
>
? S
: never;
export type Target<M extends Morphism> = M extends Morphism<
any,
infer T
>
? T
: never;
morphism.ts
We have in addition defined a Source and a Target type that can take a morphism and return its source and target, respectively. Now that we have a morphism, let's attempt to describe an isomorphism: a pair of morphisms, one forward and one inverse, in code:
import { Morphism } from "./morphism";
export type Iso<A, B> = [Morphism<A, B>, Morphism<B, A>];iso.ts
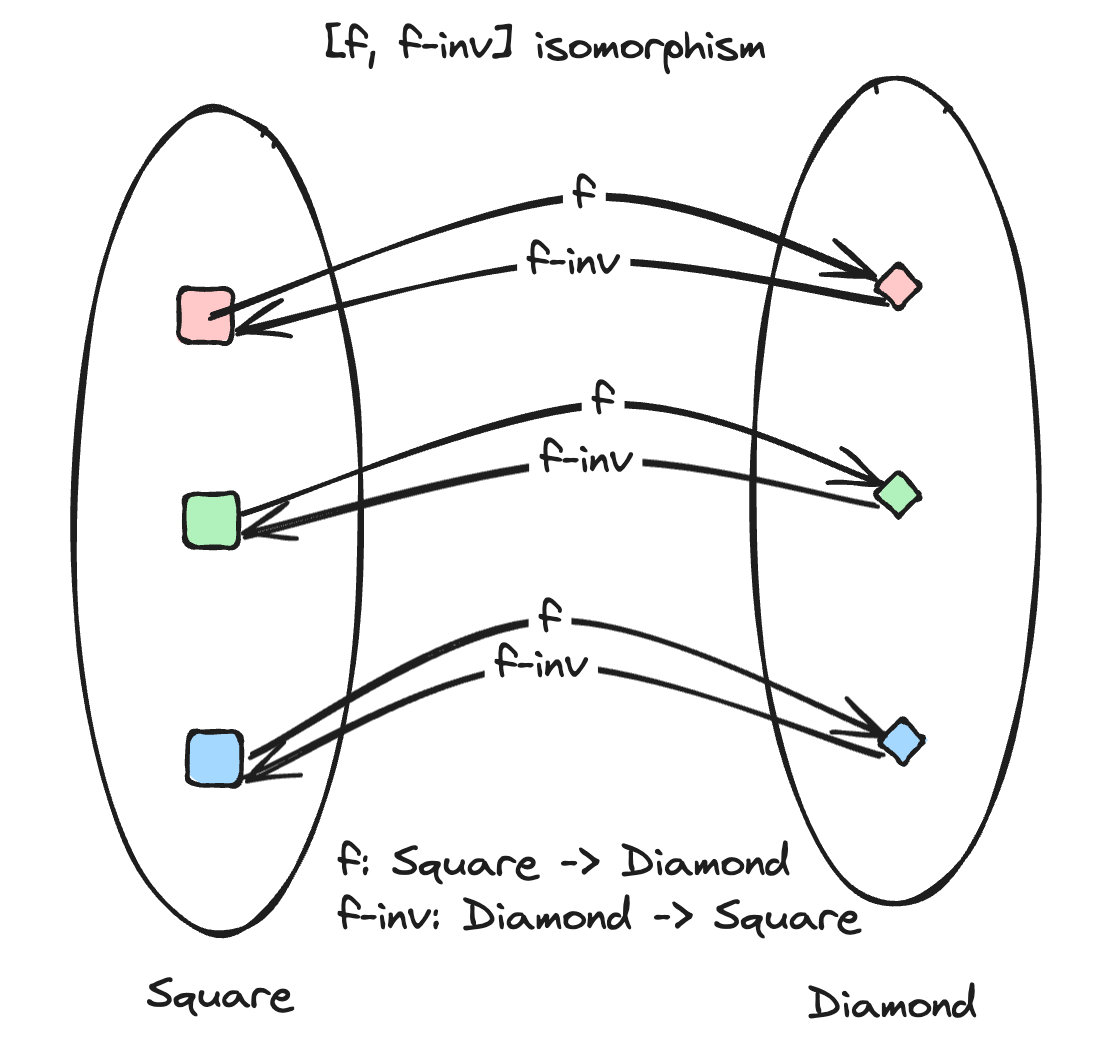
So we've defined a type Iso<A, B>. We can see that it's literally a pair of morphisms, one from A to B and another from B to A. But we can create any such pairs, and they may not be an isomorphism. The types aren't enough, there are some laws that must be true.
What makes an isomorphism?
Isomorphisms have certain properties, that need to be valid in the pairs of functions we write, so that they are indeed isomorphisms. Here are the conditions:
For a pair of morphisms f, g they are isomorphisms, if and only if the following hold true: f.g = id and g.f = id. Actually, that's it. So what do ., = and id mean?
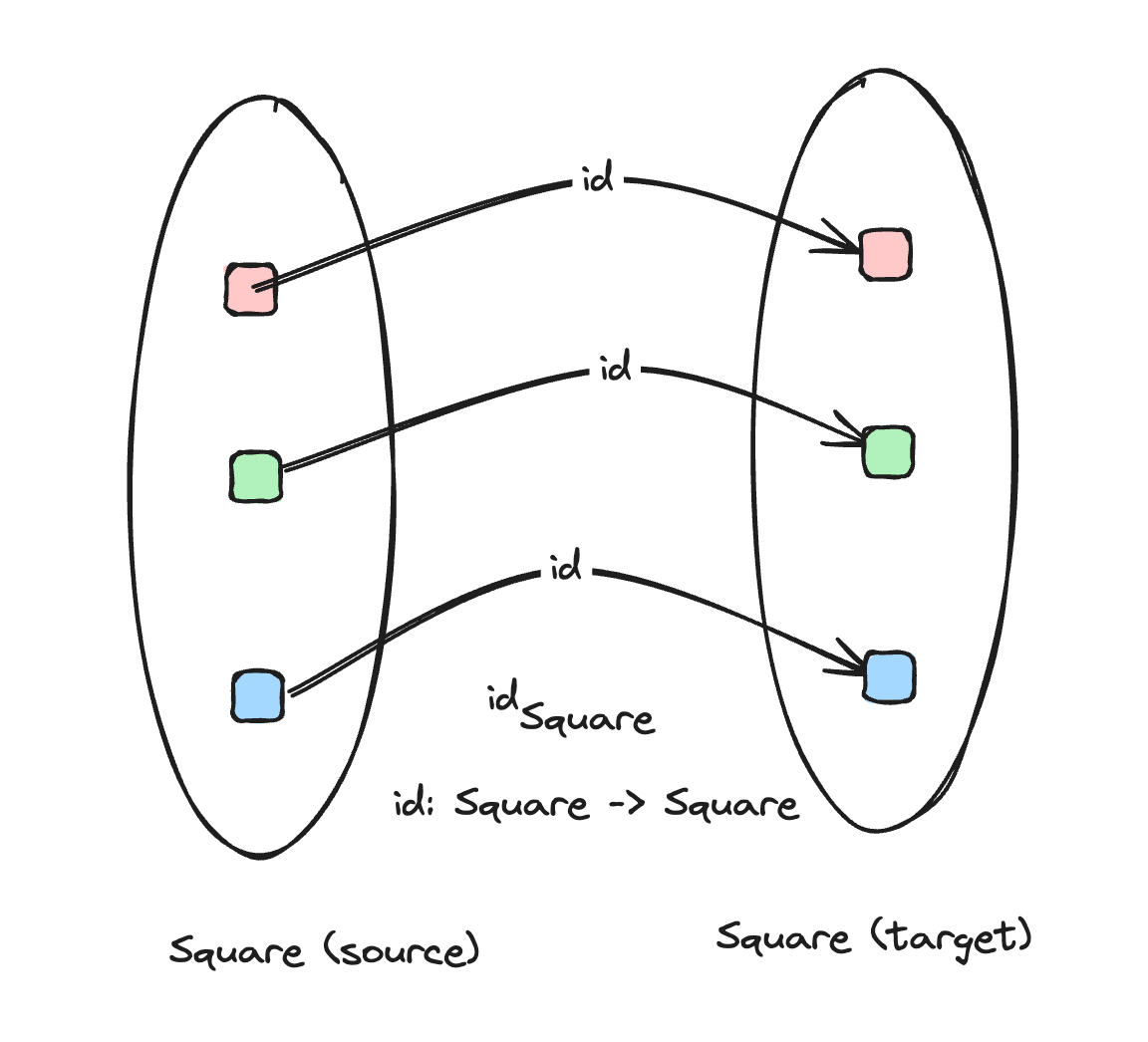
The identity morphism id
An identity morphism is simply a function that maps an object back to itself. Since the type of the object it maps can vary, it sometimes has a suffix, like: idA where A is type of object for which the identity is being referenced. We can define it thus:
import { Morphism } from "./morphism";
export type Identity<A = any> = Morphism<A, A>;
export const identity = <A = any>(a: A): A => a;
identity.ts
As we can see, it's a morphism where the source and target are identical, and in TypeScript it can be declared as a generic function that just returns the same value it got.
The composition of morphisms .
For a pair of morphisms f and g where the target of f is the same as the source of g, a composition of the morphisms is a morphism with the source of the f, and the target of the other (cancelling out the identical source and target). It also has to follow some axioms, given the identity morphism id that we just defined.
- For every morphism f from
AtoB, idB ∘ f = f = f ∘ idA - For any compatible morphisms f, g and h, h ∘ (g ∘ f) = (h ∘ g) ∘ f (compatibility here means that the compositions are defined, which means the target of f is the source of g, and the target of g is the source of h.
Given the previous example of f, if we have a g:
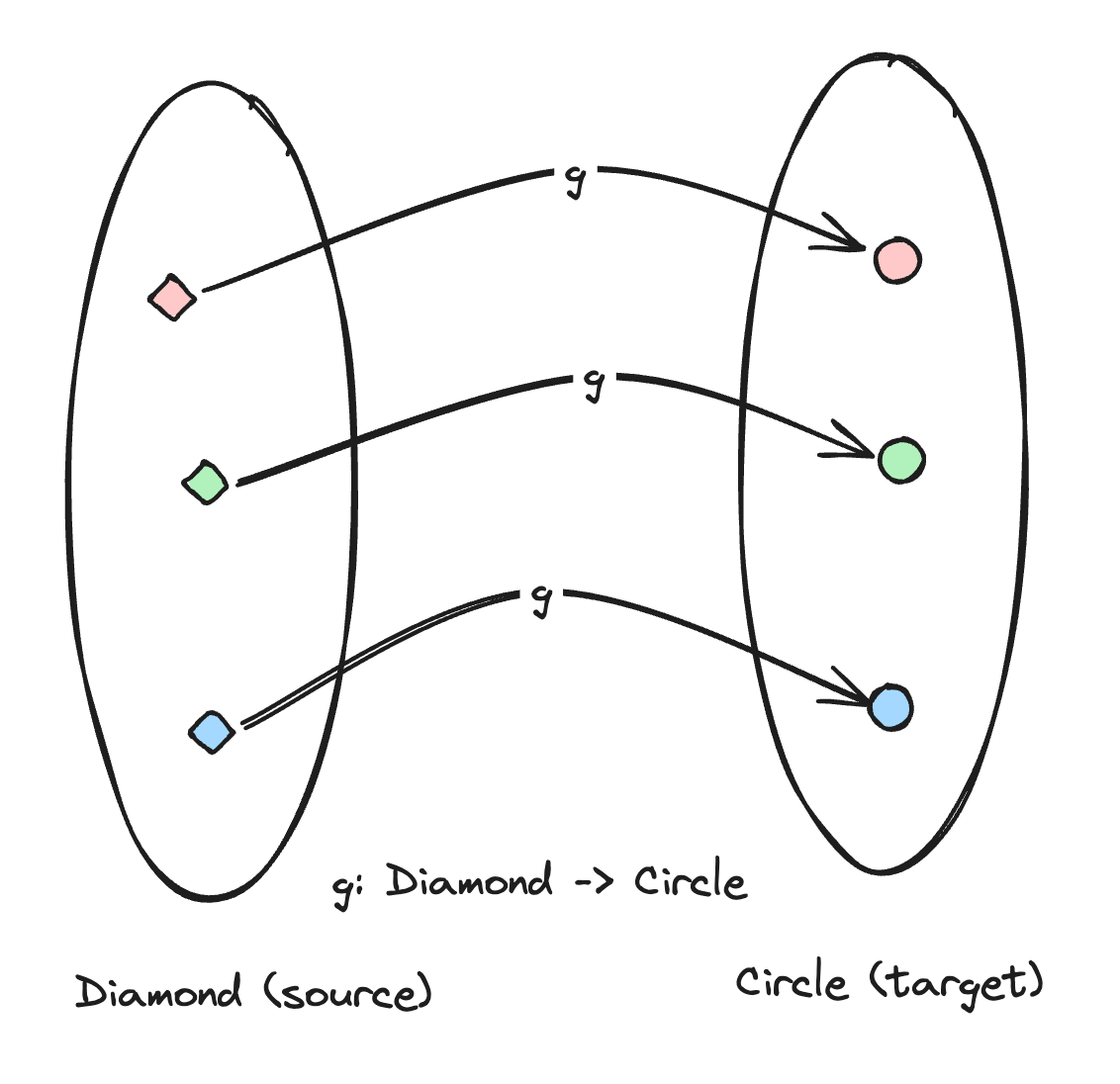
Our composition of f and g will be g . f as follows:
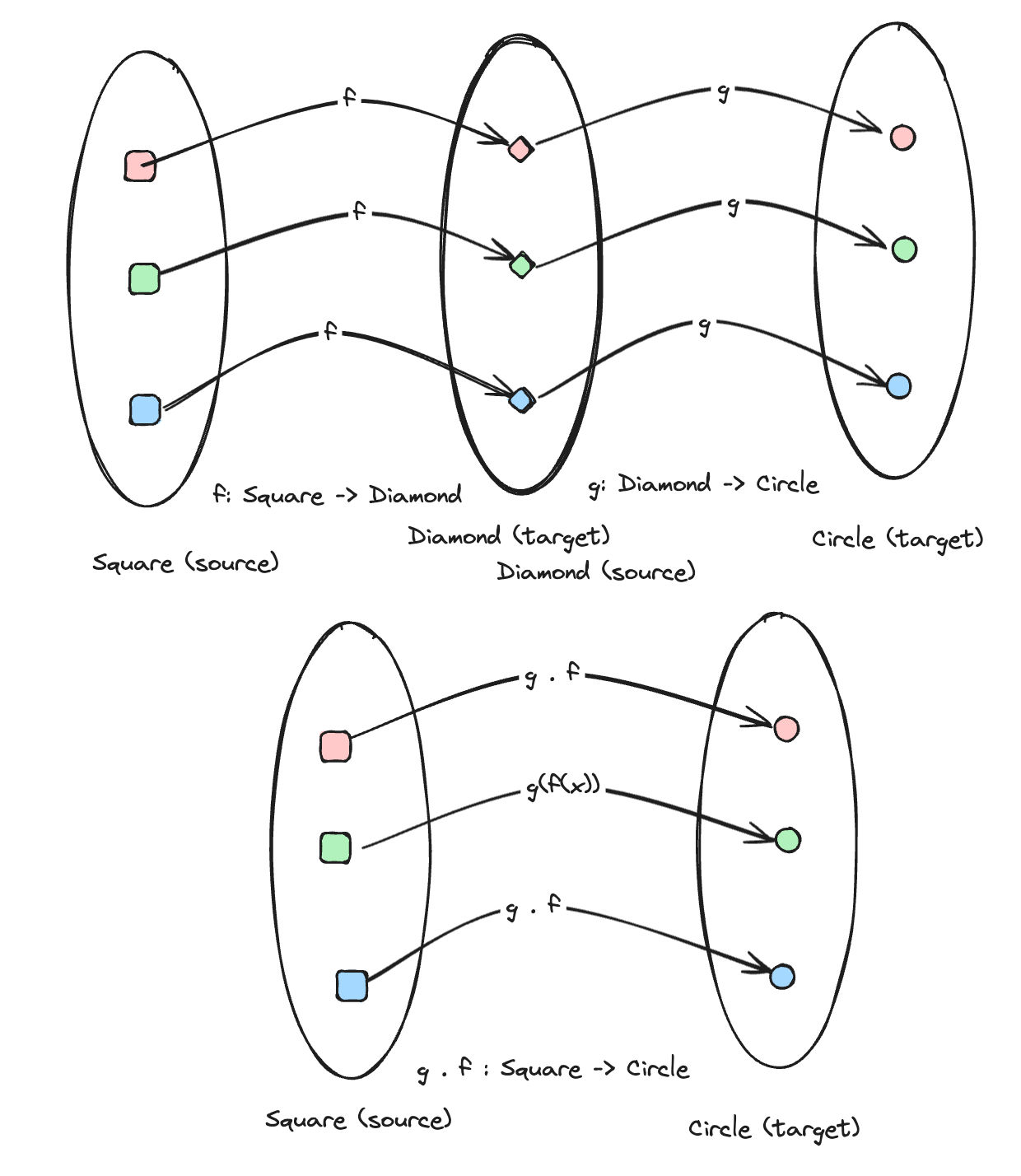
Let's write that out in TypeScript:
import { Morphism } from "./morphism";
export const compose =
<B, C>(g: Morphism<B, C>) =>
<A>(f: Morphism<A, B>): Morphism<A, C> =>
(a) =>
g(f(a));
compose.ts
As per our definition, compose(g)(f) = g ∘ f, which is right-to-left composition. This means the function on the right (f) is applied first, and the function on the left (g) is applied after (to the result of the first). We can see that the resulting function takes the form a => g(f(a)) when called as compose(g)(f). We could also write a left-to-right composition, which is typically called pipe. I'll let you work it out.
NOTE: This is a curried function. A curried function is a multivariate (having multiple variables) function that takes one argument at a time, returning other such functions until there are no more arguments left to take, at which point it returns the result. Most of the other functions I discuss in this post are also curried. This enhances reusability, composability, and expressiveness. If you have difficulties reading curried functions, please refer to my post on why I write curried functions.
Equality of morphisms =
Two morphisms are considered equal if they map the same sources to the same targets. Since equality is a test, we may want to write a test specification for this part.
First, we can express our ideas of a predicate which is a morphism with a boolean target, and an equals morphism which has a predicate target:
import { Morphism } from "./morphism";
import { List } from "./types";
export type Predicate<Arg> = Morphism<Arg, boolean>;
export type Equals<A> = Morphism<A, Predicate<A>>;
export const equals =
<A>(a: A): Predicate<A> =>
(b) =>
b === a;
export const sequence_equals =
<A>(as: List<A>): Predicate<List<A>> =>
(bs) =>
bs.length === as.length && as.every((a, i) => a === bs[i]);
predicate.ts
We define a way to describe values and lists as strictly equal. We can use the Equals type to define our equality test for 2 morphisms. We'll use the fast-check library for our property based tests, with mocha (installing types from @types/mocha):
import fc from "fast-check";
import { Morphism } from "./morphism";
import { Equals } from "./predicate";
export const equals =
<B>(equals: Equals<B>) =>
<A>(a: fc.Arbitrary<A>) =>
(f: Morphism<A, B>) =>
(g: Morphism<A, B>) =>
it(`${f.name} = ${g.name}`, () => {
// To say f = g:
// for every a, f(a) should equal g(a)
fc.assert(fc.property(a, (a) => equals(f(a))(g(a))));
});
equals.spec.ts
Given we can't test the equality of functions, we'll test whether the targets of the morphisms are considered equal, given randomly generated inputs of the source type.
We use the names of the morphism in this test, so it'd be useful to set the name of a morphism:
import { Morphism } from "./morphism";
export const named =
(name: string) =>
<A, B>(f: Morphism<A, B>): Morphism<A, B> => {
const fn = (a: A) => f(a);
Object.defineProperty(fn, "name", {
value: name,
configurable: true,
});
return fn;
};
named.ts
Specification
Given the definition of an isomorphism involves laws, axioms, and equality, it's clear we need to define a property-based test specification for isomorphisms as well, taking cue from our equals specification. Let's attempt that:
import fc from "fast-check";
import { Identity } from "./identity";
import { compose } from "./compose";
import { Iso } from "./iso";
import { Equals } from "./predicate";
import { equals } from "./equals.spec";
import { named } from "./named";
export type Type<T> = {
arb: fc.Arbitrary<T>;
eq: Equals<T>;
id: Identity<T>;
};
const gof = named("g ∘ f");
const fog = named("f ∘ g");
export const iso =
<A>(a: Type<A>) =>
<B>(b: Type<B>) =>
(iso: Iso<A, B>): void => {
const [f, g] = iso;
equals(a.eq)(a.arb)(gof(compose(g)(f)))(a.id);
equals(b.eq)(b.arb)(fog(compose(f)(g)))(b.id);
};
iso.spec.ts
We first define a Type<T> which gives us an arbitrary value generator of the type, a way to check if 2 values of the type are equal, and an identity morphism for the type. We then use named compositions of g and f to test the laws, using our equals specification. That should be enough to test isomorphisms.
The identity isomorphism
Every type has at least one isomorphism, which is the identity isomorphism. It should be really simple to see, given when we compose id with itself, we definitely get id in return. But let's use our isomorphism specification to validate:
import fc from "fast-check";
import { identity } from "./identity";
import { Type, iso } from "./iso.spec";
import { equals } from "./predicate";
describe("identity", () => {
const Integer: Type<number> = {
arb: fc.integer(),
eq: equals,
id: identity,
};
iso(Integer)(Integer)([identity, identity]);
});
identity.spec.ts
We can see that the results pass, when we run with mocha -r ts-node/register *.spec.ts after also installing ts-node:

While I wrote a test for identity isomorphism for numbers, we can also write one for any value - I'll leave that as an exercise to you.
An invalid isomorphism
Earlier, we mentioned that not all pairs of morphisms for a type are isomorphisms. A simple example can help prove that. Let's (ab)use the increment function for the nth time in my posts:
import { Morphism } from "./morphism";
import { Iso } from "./iso";
const increment: Morphism<number, number> = (x) => x + 1;
export const invalid: Iso<number, number> = [increment, increment];
invalid.ts
Notice that the type signature works, and TypeScript doesn't complain. However, that's not an isomorphism, as we can verify using our specifications for isomorphisms:
import fc from "fast-check";
import { identity } from "./identity";
import { Type, iso } from "./iso.spec";
import { equals } from "./predicate";
import { invalid } from "./invalid";
describe("invalid", () => {
const Integer: Type<number> = {
arb: fc.integer(),
eq: equals,
id: identity,
};
iso(Integer)(Integer)(invalid);
});
invalid.spec.ts
Sure enough, we can see it fail:

A few more valid isomorphisms
In order to ensure we understand, let's build a few more valid isomorphisms. These should be simple, with just a definition, and a specification. A few basic types will come in handy, and they'll make sense as we go over the examples:
export type NaturalNumber = number;
export type Square = number;
export type WholeNumber = number;
export type NumericString = string;
types.ts
The successor/predecessor isomorphism
For every whole number (which are positive integers including 0), there exists a successor natural number (which are positive integers excluding 0 and starting with 1), and for every natural number there's a predecessor whole number. We can describe this as an isomorphism:
import { Iso } from "./iso";
import { NaturalNumber, WholeNumber } from "./types";
export const successor: Iso<WholeNumber, NaturalNumber> = [
(a) => a + 1,
(b) => b - 1,
];
successor.ts
We can also see that it's an isomorphism:
import { identity } from "./identity";
import { Type, iso } from "./iso.spec";
import { equals } from "./predicate";
import { successor } from "./successor";
import fc from "fast-check";
describe("successor", () => {
const WholeNumber: Type<number> = {
arb: fc.integer({ min: 0 }),
eq: equals,
id: identity,
};
const NaturalNumber: Type<number> = {
arb: fc.integer({ min: 1 }),
eq: equals,
id: identity,
};
iso(WholeNumber)(NaturalNumber)(successor);
});
successor.spec.ts
Note that we have defined whole number and natural number using integers and a minimum value.
The square/square root isomorphism
For every natural number, its square exists as another natural number, and for every such square, its square root is also natural number. This can also be an isomorphism:
import { Iso } from "./iso";
import { NaturalNumber, Square } from "./types";
export const square: Iso<NaturalNumber, Square> = [
(a) => a * a,
(b) => Math.sqrt(b),
];
square.ts
We can also write the specification:
import fc from "fast-check";
import { identity } from "./identity";
import { Type, iso } from "./iso.spec";
import { equals } from "./predicate";
import { square } from "./square";
describe("square", () => {
const NaturalNumber: Type<number> = {
arb: fc.integer({
min: 1,
max: Math.floor(Math.sqrt(Number.MAX_SAFE_INTEGER)),
}),
eq: equals,
id: identity,
};
const SquareNumber: Type<number> = {
arb: NaturalNumber.arb.map((x) =>
Math.pow(x, 2)
),
eq: equals,
id: identity,
};
iso(NaturalNumber)(SquareNumber)(square);
});
square.spec.ts
Notice that our square number domain is restricted to the squares of natural numbers, and our natural numbers domain is restricted to the maximum value possible for which the square is a safe integer in JavaScript.
The number/numeric string isomorphism
For every natural number, there's an equivalent string representation, and for every string representation of a natural number, there's an equivalent natural number:
import { Iso } from "./iso";
import { NaturalNumber, NumericString } from "./types";
export const numeric: Iso<NaturalNumber, NumericString> = [
(a) => a.toString(),
(b) => parseInt(b, 10),
];
numeric.ts
Here's our specification:
import fc from "fast-check";
import { identity } from "./identity";
import { Type, iso } from "./iso.spec";
import { equals } from "./predicate";
import { numeric } from "./numeric";
describe("numeric", () => {
const Integer: Type<number> = {
arb: fc.integer(),
eq: equals,
id: identity,
};
const String: Type<string> = {
arb: Integer.arb.map(x => x.toString()),
eq: equals,
id: identity,
};
iso(Integer)(String)(numeric);
});
numeric.spec.ts
Notice that our domain for the string type is only string representations of integers and not all strings.
Exercise Time!
Given we've gone over isomorphisms, here's a few exercises:
- Write an isomorphism (and test it) between a list of natural numbers, and a list of numeric strings.
- Did you reuse the number/numeric string isomorphism above?
- Can you make a generic isomorphism that can traverse across lists?
- Write an isomorphism between a list of numbers and a string with comma-separated numbers.
- Did you run into any edge cases? This is why property based tests help.
- Did you reuse the number/numeric string isomorphism above?
- Write an isomorphism for curry/un-curry (without referring to my previous blog post).
Conclusion
Hope you enjoyed the post about isomorphisms. I'd encourage you to think about equivalences you might see or appreciate in real life and see if they're isomorphisms. Now that you know what the associated laws are and how we can test against them, feel free to put your knowledge to the test any time. Also, a lot of equivalences are under-appreciated, and once you learn isomorphisms, you'd be able to see more of them, and connect more of these. Have fun!