Why my functions are usually curried

In a recent post on the ordering of arguments to a function, I briefly mentioned currying (if you don't know what that is, don't worry, we get there). However a lot of people that work with me know that my functions are usually curried. Those that work with me, or look at my code, or review it, generally have their own preferences. Some people are annoyed as they don't like it, and others are surprised as they've not seen it before. It just occurred to me as a fine topic to write about, especially given it will be another helpful place I can send people to instead of having to talk about it again and again. By the end of this post, I also hope that you're able to read a curried function in whatever way you prefer, and you're no longer scared or appalled at one.

Isomorphisms

Before we go any further, I want to introduce the concept of isomorphisms. There are so many things written upon this subject, but I'd like to write a few words about it anyway. I learn by building up ideas or breaking down something complex into smaller pieces. If you need the smaller bits, you'd want to learn about a morphism, or a mapping, an injection, surjection, bijection, inversion, and finally isomorphism which is a morphism that supports an inverse morphism. I hope to someday also build up the idea of an isomophism from smaller ideas. For now, the following should suffice. Simply put, an isomorphism is a structural equivalence between objects in two different categories. Which means that, if there's an isomorphism between 2 objects, for all intents and purposes (under consideration), they're the same.

Functions

In mathematics, a function is defined as a one-to-one mapping from set X to a set Y. The set X is called the domain, and the set Y the codomain. We denote this as
f: X -> Y
We also can write the relation, for example,
f(x) = 2x
or as
f: x |-> 2x

For most of programming (with pure functions), this holds. In programming, we use types as representative sets (for example number is a type, but it also represents the set of all possible numbers in TypeScript). The input type is called the domain, and the output type, the codomain.

Here's a simple function, with a number domain and a string codomain:

export const toString = (a: number): string => a.toString();

We can say it maps numbers to strings. Here's one with number being both domain and codomain:

export const square = (a: number): number => a * a;

Can you identify the domain and codomain of this function?

export const size = <A>(as: A[]): number => as.length;

Multivariate functions

Those are just functions which take a single argument. But in mathematics, we also see functions that have more than one variable: f(x, y) = x + y. These are called multi-variate functions. That one was add. If we were to write it in TypeScript, we'd write:

export const sum = (x: number, y: number): number => x + y;

Didn't we just say that a function is a mapping from a set X to set Y? What then is the domain of this function? Well, for multivariate functions, for a function of n variables, the domain is a set of n-tuples (which is a heterogenous array of fixed size n). For this specific function, it's the set of all ordered pairs of numbers. The codomain is still number. What does that look like? Well, the domain is actually [number, number] - a tuple (which is a fixed size heterogenous array) of size 2 where both elements are of type number.

Here's another function with a similar domain of [number, number]:

export const product = (x: number, y: number): number => x * y;

Can you identify the domain of this function?

export const append = <A>(a: A, as: A[]): A[] => [...as, a];

Multivariate function definitions

In programming in general, there are 4 ways to define a multivariate function. Let's look at them:

n-ary

The first obvious and simplest way to write a multivariate function is to write an n-ary function, which is nothing but a function that takes n arguments. Let's take the sum example:

export const sum = (addendum: number, value: number): number =>
  value + addendum;

This doesn't clearly specify the domain (although it's simple to derive). Another characteristic is that this doesn't allow for composition or partial application (as easily as some of the later methods we'll encounter).

n-tuple

The other simple way is to model the domain exactly as it would be in mathematical terms, using an n-tuple which preserves the order. To rewrite the sum example:

export const sum = ([addendum, value]: [
  number,
  number
]): number => value + addendum;

We can also use preserve the names in the type specification:

export const sum = ([addendum, value]: [
  addendum: number,
  value: number
]): number => value + addendum;

Another version is to extract the type specification into an alias:

type SumArgs = [addendum: number, value: number];

export const sum = ([addendum, value]: SumArgs): number =>
  value + addendum;

As you may have noticed, identifying the domain is all too easy, as it's explicitly specified. Such a type is called a product type (which is a cartesian product of multiple types). This has a disadvantage of new array allocations at call sites, and also a de-structuring in the function itself.

wrapped

Another way is to wrap the argument data into an object preserving the argument names and use the object as a single argument to the function. To explain with the sum example:

export const sum = ({
  addendum,
  value,
}: {
  addendum: number;
  value: number;
}): number => value + addendum;

Another way is to write the type out explicitly as an alias:

type SumArgs = {
  addendum: number;
  value: number;
};

export const sum = ({ addendum, value }: SumArgs): number =>
  value + addendum;

We can see that this is similar to the n-tuple version in that the domain is a product type, except instead of being a position-based tuple, it's a key-based map. It also requires new object allocations at call sites and de-structuring in the function itself.

curried

Lastly, we can write curried functions, which take one argument at a time, and return the result when all the arguments have been supplied. As an example, we can write sum as:

export const sum =
  (addendum: number) =>
  (value: number): number =>
    value + addendum;

In this version, sum has different domain and codomain compared to the rest. Can you identify them? Yes, the domain is now just a number. And the codomain is a function, for which the domain is number and the codomain is also number. It offers the flexibility of partial application and composition. In some languages and runtimes which are not optimised for currying, this increases the call stack linearly with the number of arguments. It also stresses (makes more pronounced) the advantages of the order of the function arguments.

Multivariate function isomorphisms

Before we get into why my functions are usually curried, I want to establish that the different definitions mentioned above are isomorphic. We can freely change one to the other in a lossless manner while being functionally equivalent. There may be other concerns like performance, readability, and the like which may change, but they are functionally equivalent. Let's see how we can translate between the variants in a type-safe and lossless manner.

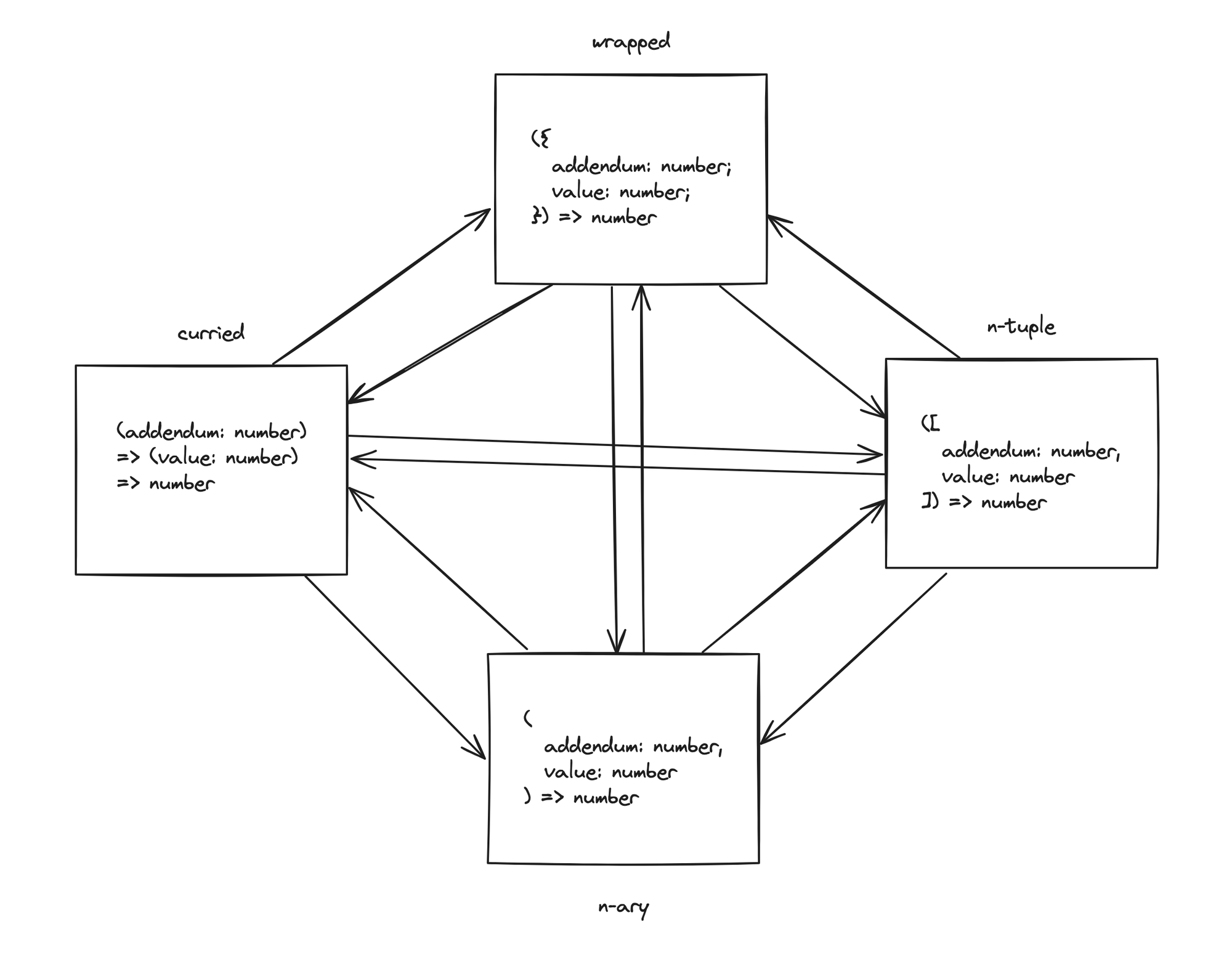
Types

Before we can create transformations, we need to represent these different versions of a multivariate function. We'll start with a simple type for an n-ary function:

export type NAry<Args extends any[], Result> = (
  ...args: Args
) => Result;

We say that an NAry is a function takes any number of args, and returns a result. These are both generic to support any type of n-ary function. Next, we can write an NTuple type. It needs to support the same generic parameters:

export type NTuple<Args extends any[], Result> = NAry<
  [Args],
  Result
>;

An NTuple for the same args just takes one tuple as its single argument, so we can define it using NAry. Moving on to the Curried type, which as usual should support the same generic parameters:

export type Curried<Args extends any[], Result> = Args extends []
  ? Result
  : Args extends [any, ...infer Tail]
  ? Args extends [...infer Head, ...Tail]
    ? NAry<Head, Curried<Tail, Result>>
    : never
  : never;

Again, we see that it can be defined using NAry. We use some type gymnastics here to get the name of the function parameters by inferring Head separately from Tail, but otherwise this is fairly straightforward. We first check if there are no arguments left - if so, we return the Result type. If not, we need to take the first element from the Args tuple, and separate it from the rest, and use it as the sole argument to an NAry function. The result of that function is the Curried<Tail, Result>. Similarly we can write the type of the Wrapped function:

export type Wrapped<
  Arg extends Record<string, any>,
  Result
> = NAry<[Arg], Result>;

Notice that the Arg type now has a constraint that it has to be a Record with string keys. It also can be expressed as an NAry function with a single argument, just like the NTuple variant. These 2 can be seen as name-mapped (for wrapped) and position-mapped (for n-tuple) arguments.

Now that we have the types, let's see them in action with the isomorphisms. We already saw a few equivalent definitions above, when we talked about the different types. Now we'll look at how we can use TypeScript to automatically translate between these variants in a lossless and type-safe manner:

n-ary <-> n-tuple

Given we have the types defined, here's the forward and inverse transforms for our isomorphism:

const to_n_tuple =
  <Args extends any[], Result>(
    f: NAry<Args, Result>
  ): NTuple<Args, Result> =>
  (args) =>
    f(...args);

const from_n_tuple =
  <Args extends any[], Result>(
    f: NTuple<Args, Result>
  ): NAry<Args, Result> =>
  (...args) =>
    f(args);

We can test these out using our sum function:

const sum = (addendum: number, value: number) =>
  value + addendum;

const n_tuple_sum = to_n_tuple(sum);
console.log(n_tuple_sum([1, 2])); // 3

const n_ary_sum = from_n_tuple(n_tuple_sum);
console.log(n_ary_sum(1, 2)); //3

We will find that the code not only type checks, but retains the names for the function arguments. We can also write the other version by hand, as we showed earlier.

n-ary <-> curried

It's a little more complicated for curried, but it's still possible:

const curry = <Args extends any[], Result>(
  f: NAry<Args, Result>
): Curried<Args, Result> =>
  f.length <= 1
    ? (f as Curried<Args, Result>)
    : (((arg: any) =>
        curry((f as Function).bind(null, arg))) as Curried<
        Args,
        Result
      >);

const uncurry =
  <Args extends any[], Result>(
    f: Curried<Args, Result>
  ): NAry<Args, Result> =>
  (...args) =>
    args.reduce((f, arg) => f(arg), f);

We use the previously discussed bind for creating a curried version which applies arguments one by one to the initial function, and reduce for creating an un-curried version which repeatedly applies the arguments to a function. We can test the above using our sum function:

const sum = (addendum: number, value: number) =>
  value + addendum;

const add = curry(sum);
console.log(add(1)(2)); // 3

const inc = add(1);
const dec = add(-1);
console.log(inc(4)); // 5
console.log(dec(4)); // 3

We will find that the code for curry not only type checks, but retains the names of the function arguments, and also executes correctly. In addition (pun intended), it neatly allows partial application, allowing us to create more useful versions of the same function by fixing the values for certain arguments. This is the simplest way to create other useful functions like inc(rement) and dec(rement) while reusing add effectively. We can also in pipelines like those created by pipe or compose, add 5 to any number by calling add(5), and using the function that it returns to transform a number.

While the uncurry code type-checks, TypeScript doesn't agree or infer the argument correctly as a curried type:

const n_ary_sum_again = uncurry(add); // Fail

We can see that we need to specify the type when we uncurry to get it to work:

const n_ary_sum_again = uncurry<
  [addendeum: number, value: number],
  number
>(add); // Works!

console.log(n_ary_sum_again(1, 2)); //3

We can also use the parameter and return type of add directly to get TypeScript to agree with the type and provide the right inference:

const n_ary_sum_again = uncurry<
  Parameters<typeof add>,
  ReturnType<typeof add>
>(add); // Works!

console.log(n_ary_sum_again(1, 2)); //3

It's better to have TypeScript auto-specify the types, so if you like me would like TypeScript to come up with the types, we can do a little more work:

type Concat<Prefix extends any[], Suffix extends any[]> = [
  ...Prefix,
  ...Suffix
];

type Uncurried<
  Function extends NAry<any, any>,
  PreviousArgs extends any[] = []
> = Function extends NAry<infer Args, infer Result>
  ? Result extends NAry<any, any>
    ? Uncurried<Result, Concat<PreviousArgs, Args>>
    : NAry<Concat<PreviousArgs, Args>, Result>
  : never;

const uncurry = <Function extends NAry<any, any>>(
  f: Function
): Uncurried<Function> =>
  ((...args) =>
    args.reduce((f, arg) => f(arg), f)) as Uncurried<Function>;

Now, we've rewritten the uncurry function to use a specific Uncurried type which recursively builds up the arguments for the final NAry to be returned. This should work:

const n_ary_sum_again = uncurry(add); // Works!

console.log(n_ary_sum_again(1, 2)); //3

We'll find that not only does the code type check and execute, but it also retains the names of the function arguments, just like we wanted.

n-tuple <-> curried

When we have an A <-> B isomorphism and A <-> C isomorphism, B <-> C is a given. I think we can safely say these are isomorphic due to the above proofs. A simple way is to use compose or pipe from the previous blog post to chain the transforms together. Basically, by combining A -> B and B -> C we get A -> C. But we can also avoid rework and do it in a single atomic step. I'll leave it as an exercise for you to come up with these transforms on your own.

* <-> wrapped

At the moment, in TypeScript, there's no way to come up with the wrapped isomorphisms with the other types dynamically due to the function argument names not being captured in the type system for any meaningful use. It is definitely possible to hand-craft a wrapped version which is isomorphic like we did in the above examples with sum, so I hope that serves as enough justification for why it's isomorphic with the rest. To give a general rule of thumb, we basically take the function argument names in order and use them as keys while retaining their types in the argument object. For the inverse, we simple iterate over the key-type pairs in the object type and rewrite them as function arguments to an n-ary function. Translating that into other types is already discussed.

Which is the best?

Of the several ways to specify a multivariate function, I find that the curried version is the most useful. This is primarily because of how easy functions are to compose and use in pipelines once it's curried. It also promotes (makes easy) partial application. For examples, you'll find the rest of my posts use a lot of curried functions, like the remainder and isDivisibleBy functions in my last post. In future posts, we will also come across certain cases where the partial application promoted by currying becomes very useful to succinctly express powerful abstractions. Every function taking a single argument massively simplifies how we can think about and interact with functions. Hopefully you're no longer scared of curried functions, and can read them in whatever way works best for you, given it's just 1 of 4 ways to write a multivariate function.

As I always mention, there's a cost to using abstractions, and it's usually performance. When considering the right way to specify a multivariate function, think carefully about how likely you are to partially apply arguments to a function and its utility. It's less useful for a function to be curried when it's always supplied with all its arguments. Conversely, it's less useful for a function to expect all its arguments when it's usually built up gradually.

As for me, I've mostly found that having the curried version of the function enables the most flexibility, and I ultimately find ways to take advantage of it. It works really well with the way I think and build solutions, which is using simple ideas and putting them together gradually. See if you can make use of it where it makes sense, and hopefully you're able to see the power and flexibility of curried functions!

The code above is available in an interactive TS playground